[单选]

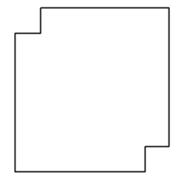
劳动技能课上老师给出一道手工题：一张正方形纸片，在一对对角处各减去一个边长为1厘米的小正方形（如下图所示），想办法把这个缺角的正方形恰好剪成一些长2厘米、宽1厘米的小矩形，问初始的大正方形边长要多大时，任务才有可能完成？

A . 8
B . 15
C . 32
D . 以上答案都不对

　　---------------------------------

　　参考答案：D

　　---------------------------------

　　[华图教育参考解析]：

第一步：判断题型------本题为几何问题

第二步：分析作答：
将初始的大正方形分成n×n个边长为1的小正方形：

 如上图所示，若将这些小正方形黑白间隔染色，所得到的黑白方格的数量是一样的；
而长2、宽1的小矩形必须由一个黑格和一个白格组成，即、，由2个白格或者2个黑格，其构成的图形只能为、；
所以只要缺角的正方形即题目中所给图形其剩下的方格满足黑格数等于白格数，就能恰好剪成一些长2厘米、宽1厘米的小矩形；
在完好的大正方形中，黑格数=白格数；
在缺角的正方形中，因为剪去的是互为对角的2个小正方形，观察上图即可发现，互为对角的2个小正方形颜色相同，所以减掉后必然会少2个白格或2个黑格，导致剩下的白格和黑格的数量不等；
而白格和黑格数量不等就不能恰好全都构成矩形，因为长2、宽1的小矩形必须由一个黑格和一个白格组成；
因此无论大正方形的边长是多少，只要减掉2个互为对角的小正方形，就不能实现题中分割，所以A、B、C选项均不对。

故本题选D。
【2018-内蒙古-065】